The Tautochrone Problem - Why the Cycloid is Isochronous

What we’re trying to prove:

A particle sliding down a cycloid under gravity, considering friction to be non-existent will take the same time to reach the lowest point regardless of its starting point on the curve.

Cycloid?

A cycloid is the curve traced by a point on the rim of a rolling circle.

Consider the radius of this circle to be r.

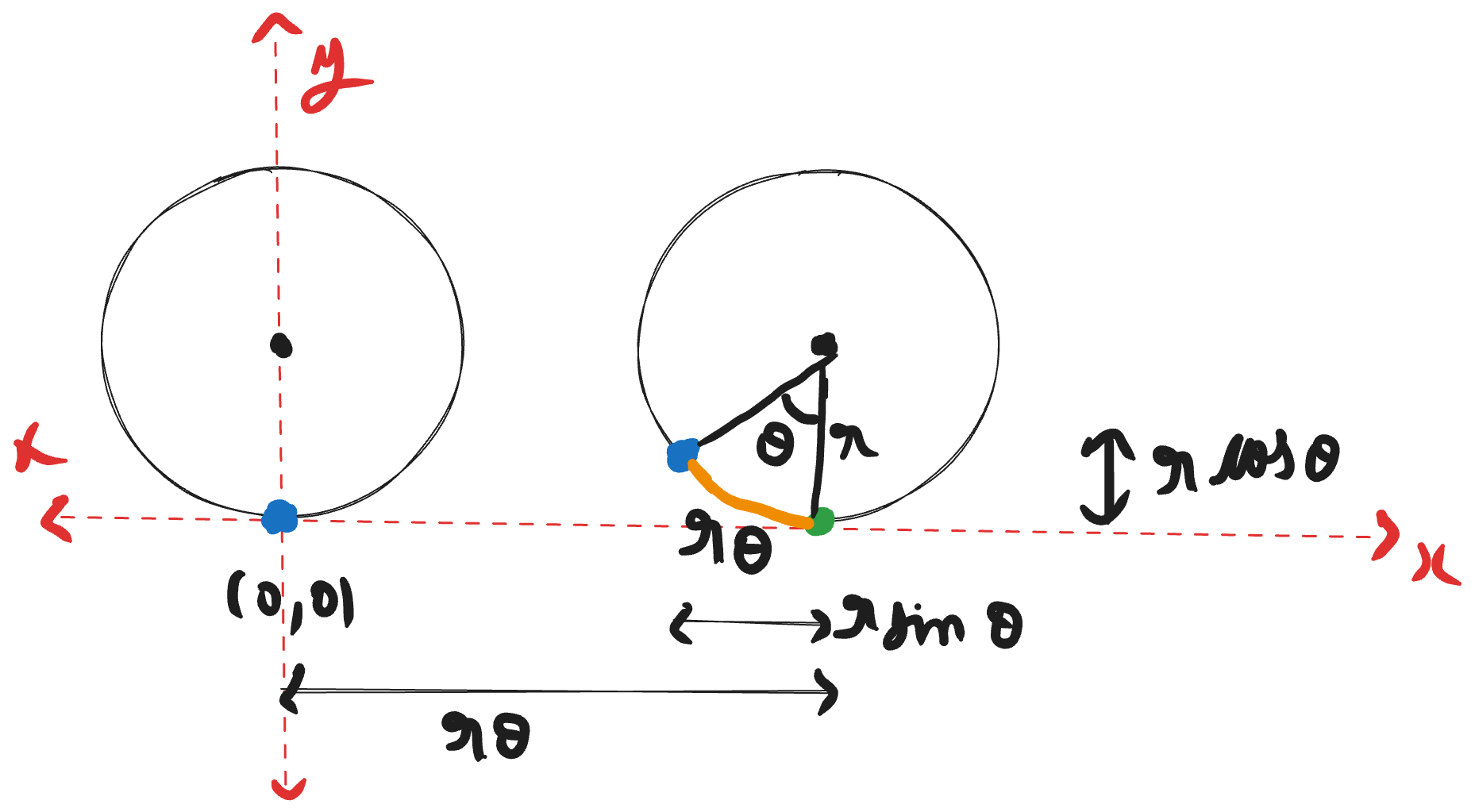
From the diagram, we can clearly see that:

$$x=r(\theta -\sin \theta )$$ $$y=r(1-\cos \theta )$$

From which we get:

$$\frac{dx}{d\theta }=r(1-cos\theta )$$ $$\frac{dy}{d\theta }=r\sin \theta$$

For any curve:

$$ds=\sqrt{(dx{)}^2+(dy{)}^2}$$ $$ds=\sqrt{(\frac{dx}{d\theta }{)}^2+(\frac{dy}{d\theta }{)}^2}d\theta$$ $$ds=r\sqrt{(1-cos\theta {)}^2+{\sin }^2\theta }d\theta$$ $$ds=r\sqrt{2(1-\cos \theta )}d\theta$$

We know that:

$$dt=\frac{ds}{v}$$

From energy conservation, $v=\sqrt{2g(y-y_0)}$

$$dt=r\sqrt{\frac{1-\cos \theta }{g(y-y_0)}}d\theta$$

Substituting $y=r(1-\cos \theta )$ and $y_0=r(1-\cos {\theta }_0)$

$$dt=r\sqrt{\frac{1-\cos \theta }{gr(\cos {\theta }_0-\cos \theta )}}d\theta$$ $$dt=\sqrt{\frac{r}{g}}\sqrt{\frac{1-\cos \theta }{\cos {\theta }_0-\cos \theta }}d\theta$$

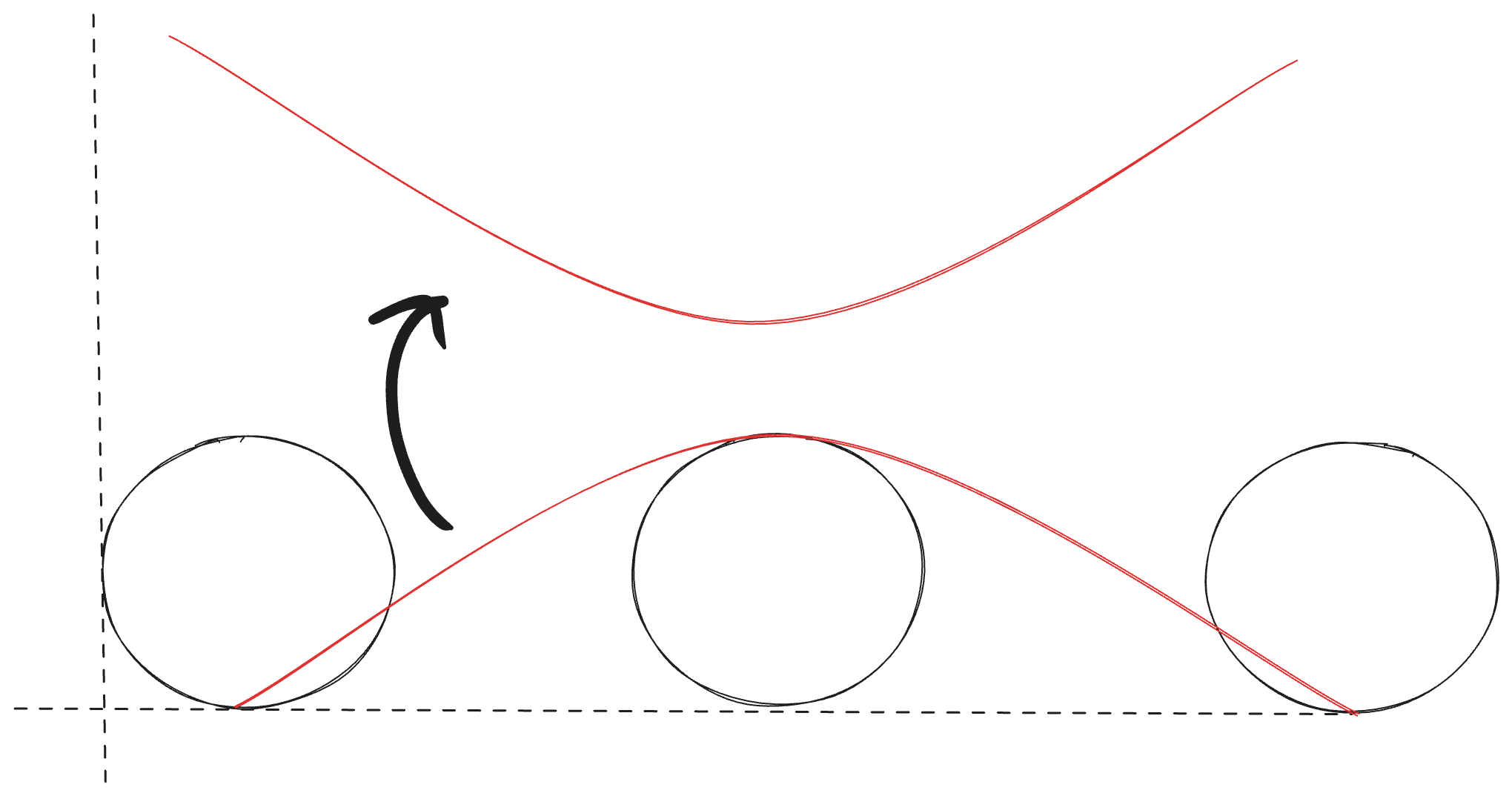
It is very important to note here that in this problem, we consider the cycloid to be inverted. Therefore, we interpret y as the depth BELOW the starting point and not the height above the ground.

In other words, we treat y = 0 as the top of the curve and y = 2r as the bottom. Therefore, $\theta =\pi$ for the bottom. It is not 0.

So when we integrate to get the time of descent we take the upper limit to be $\pi$ and the lower limit to be ${\theta }_0$ which is arbitrary.

$$T=\sqrt{\frac{r}{g}}{\int }_{{\theta }_0}^{\pi }\sqrt{\frac{1-\cos \theta }{\cos {\theta }_0-\cos \theta }}d\theta$$ $$T=\sqrt{\frac{r}{g}}{\int }_{{\theta }_0}^{\pi }\sqrt{\frac{2{\sin }^2\frac{\theta }{2}}{2({\cos }^2\frac{{\theta }_0}{2}-{\cos }^2\frac{\theta }{2})}}d\theta$$ $$T=\sqrt{\frac{r}{g}}{\int }_{{\theta }_0}^{\pi }\frac{\sin \frac{\theta }{2}}{\sqrt{{\cos }^2\frac{{\theta }_0}{2}-{\cos }^2\frac{\theta }{2}}}d\theta$$ $$T=\sqrt{\frac{r}{g}}{\int }_{{\theta }_0}^{\pi }\frac{\frac{\sin \frac{\theta }{2}}{\cos \frac{{\theta }_0}{2}}}{\sqrt{1-(\frac{\cos \frac{\theta }{2}}{\cos \frac{{\theta }_0}{2}}}{)}^2}d\theta$$

Let $u=\frac{\cos \frac{\theta }{2}}{\cos \frac{{\theta }_0}{2}}$ and $du=\frac{-\sin \frac{\theta }{2}}{2\cos \frac{{\theta }_0}{2}}d\theta$ Replacing $d\theta$ with $du$ and substituting $u$ in the equation, we get:

$$T=2\sqrt{\frac{r}{g}}{\int }_{{\theta }_0}^{\pi }\frac{-1}{\sqrt{1-u^2}}du$$ $$T=2\sqrt{\frac{r}{g}}[\arccos (u){]}_{{\theta }_0}^{\pi }$$ $$T=2\sqrt{\frac{r}{g}}[\arccos (\frac{\cos \frac{\theta }{2}}{\cos \frac{{\theta }_0}{2}}){]}_{{\theta }_0}^{\pi }$$ $$T=2\sqrt{\frac{r}{g}}(\arccos (0)-\arccos (1))$$ $$T=\pi \sqrt{\frac{r}{g}}$$

Therefore, we can see that the time of descent is not dependent on the initial angle ${\theta }_0$.

This property, that all particles reach the bottom simultaneously regardless of their starting point is known as isochronism and it’s what makes the cycloid the solution to the Tautochrone problem.